(本小题满分14分) 函数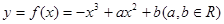 .
.
(1)要使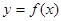 在(0,1)上单调递增,求
在(0,1)上单调递增,求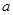 的取值范围;
的取值范围;
(2)当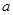 >0时,若函数满足
>0时,若函数满足 =1,
=1, =
=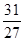 ,求函数
,求函数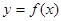 的解析式;
的解析式;
(3)若x∈[0,1]时,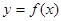 图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
图象上任意一点处的切线倾斜角为θ,求当0≤θ≤ 时
时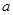 的取值范围.
的取值范围.
推荐套卷
(本小题满分14分) 函数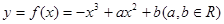 .
.
(1)要使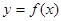 在(0,1)上单调递增,求
在(0,1)上单调递增,求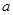 的取值范围;
的取值范围;
(2)当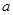 >0时,若函数满足
>0时,若函数满足 =1,
=1, =
=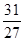 ,求函数
,求函数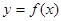 的解析式;
的解析式;
(3)若x∈[0,1]时,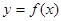 图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
图象上任意一点处的切线倾斜角为θ,求当0≤θ≤ 时
时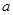 的取值范围.
的取值范围.