如图，已知抛物线y＝ax2＋bx＋4与x轴交于A（－2,0）、B两点，与y轴交于C点，其对称轴为直线x＝1.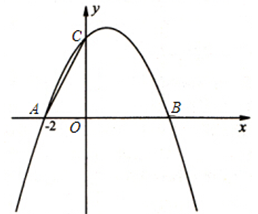
（1）直接写出抛物线的解析式 ：
（2）把线段AC沿x轴向右平移，设平移后A、C的对应点分别为A′、C′，当C′落在抛物线上时，求A′、C′的坐标；
（3）除（2）中的点A′、C′外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形，若存在，求出E、F的坐标；若不存在，请说明理由.
相关试题
如图，已知在△ABC中，∠A=90°
（1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）．
（2）若∠B=60°，AB=3，求⊙P的面积．
如图，在边上为1个单位长度的小正方形网格中：
（1）画出△ABC向上平移6个单位长度，再向右平移 5个单位长度后的△A1B1C1．
（2）以点B为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2．
（3）求△CC1C2的面积．
的一个根,求
的值．
相关知识点
推荐套卷
粤公网安备 44130202000953号