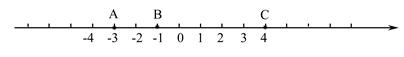点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
(1)数轴上表示1和5两点之间的距离是 ,数轴上表示2和-1的两点之间的距离是 ;
(2)数轴上表示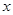 和-1的两点之间的距离表示为 ;
和-1的两点之间的距离表示为 ;
(3)若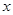 表示一个有理数,且
表示一个有理数,且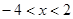 ,则
,则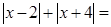 ;
;
(4)利用数轴求出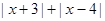 的最小值,并写出此时
的最小值,并写出此时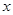 可取哪些整数值?(4 分)
可取哪些整数值?(4 分)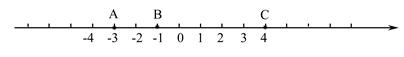
相关知识点
推荐套卷
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
(1)数轴上表示1和5两点之间的距离是 ,数轴上表示2和-1的两点之间的距离是 ;
(2)数轴上表示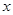 和-1的两点之间的距离表示为 ;
和-1的两点之间的距离表示为 ;
(3)若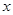 表示一个有理数,且
表示一个有理数,且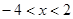 ,则
,则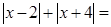 ;
;
(4)利用数轴求出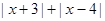 的最小值,并写出此时
的最小值,并写出此时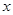 可取哪些整数值?(4 分)
可取哪些整数值?(4 分)