如图，在平面直角坐标系中，O为原点，每个小方格的边长为1个单位长度．在第一象限内有横、纵坐标均为整数的A、B两点，且OA= OB=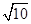
．
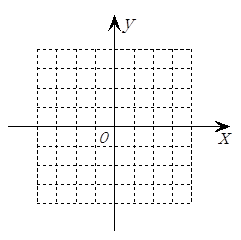
（1）写出A、B两点的坐标；
（2）将线段AB绕点O旋转一周，求所形成的图形的面积（结果保留π）．
相关试题
，（其中x≠0）相关知识点
推荐套卷
如图，在平面直角坐标系中，O为原点，每个小方格的边长为1个单位长度．在第一象限内有横、纵坐标均为整数的A、B两点，且OA= OB=．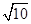
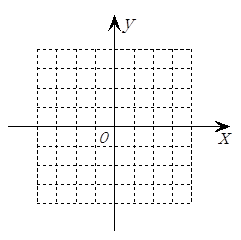
（1）写出A、B两点的坐标；
（2）将线段AB绕点O旋转一周，求所形成的图形的面积（结果保留π）．
粤公网安备 44130202000953号