如图所示，过正方形ABCD的中心O作OP⊥平面ABCD，已知正方形的边长为2，OP=2，连接AP、BP、CP、DP，M、N分别是AB、BC的中点，以O为原点，射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系．若E、F分别为PA、PB的中点，求A、B、C、D、E、F的坐标．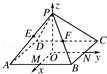
相关试题
是圆
上的动点，
的取值范围
恒成立，求实数
的取值。
，满足
的解析式
时，求函数
的值是5，则输出的
值是多少？
（
为参数）被双曲线
所截得的弦长。
的值；
，求
的值；
在
上的最小值．推荐套卷
如图所示，过正方形ABCD的中心O作OP⊥平面ABCD，已知正方形的边长为2，OP=2，连接AP、BP、CP、DP，M、N分别是AB、BC的中点，以O为原点，射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系．若E、F分别为PA、PB的中点，求A、B、C、D、E、F的坐标．
粤公网安备 44130202000953号