已知函数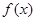 满足对任意实数
满足对任意实数 都有
都有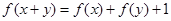 成立,且当
成立,且当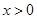 时,
时,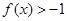 ,
,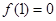 .
.
(1)求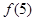 的值;
的值;
(2)判断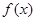 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数 ,总能找到一个正实数
,总能找到一个正实数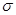 ,使得当
,使得当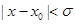 时,
时, ,则称函数
,则称函数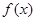 在
在 处连续。试证明:
处连续。试证明: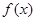 在
在 处连续.
处连续.
推荐套卷
已知函数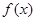 满足对任意实数
满足对任意实数 都有
都有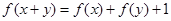 成立,且当
成立,且当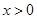 时,
时,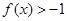 ,
,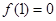 .
.
(1)求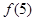 的值;
的值;
(2)判断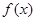 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数 ,总能找到一个正实数
,总能找到一个正实数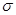 ,使得当
,使得当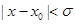 时,
时, ,则称函数
,则称函数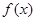 在
在 处连续。试证明:
处连续。试证明: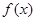 在
在 处连续.
处连续.