设椭圆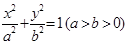
的左、右焦点分别为F1，F2，右顶点为A，上顶点为B.已知|AB|＝
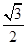|F1F2|.
（1）求椭圆的离心率；
（2）设P为椭圆上异于其顶点的一点，以线段PB为直径的圆经过点F1，经过原点O的直线l与该圆相切，求直线l的斜率．
相关试题
与椭圆
有相同的焦点，直线
是双曲线
的直线
与双曲线
、
两点，若
,求直线
中， 
，且
.
的前
项和
.
中，角
所对的边分别为
，已知
，
，
．
的值； 
的值．
的不等式
.推荐套卷
设椭圆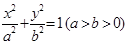 的左、右焦点分别为F1，F2，右顶点为A，上顶点为B.已知|AB|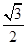＝|F1F2|.
（1）求椭圆的离心率；
（2）设P为椭圆上异于其顶点的一点，以线段PB为直径的圆经过点F1，经过原点O的直线l与该圆相切，求直线l的斜率．
粤公网安备 44130202000953号