如图，直角坐标系XOY中，点F在x轴正半轴上，
的面积为S.且
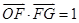，设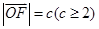
，
.
（1）以O为中心，F为焦点的椭圆E经过点G，求点G的纵坐标.
（2）在（1）的条件下，当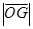
取最小值时，求椭圆E的标准方程.
（3）在（2）的条件下，设点A、B分别为椭圆E的左、右顶点，点C是椭圆的下顶点，点P在椭圆E上（与点A、B均不重合），点D在直线PA上，若直线PB的方程为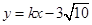
，且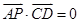
，试求CD直线方程.
相关试题
,当
为何值时，
与
垂直？
与
是第三象限角，且
.
的值;
的值
的前
项和为
，对任意的正整数
成立，记
。
的通项公式；
，设数列
的前
，求证：对任意正整数
；
在区间
上有且只有一个零点，求实数
的取值范围。
为公差不为零的等差数列，首项
，
、
、 、
恰为等比数列，且
，
，
．
；
的前
项和为
，求推荐套卷
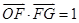如图，直角坐标系XOY中，点F在x轴正半轴上，的面积为S.且，设，.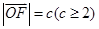
（1）以O为中心，F为焦点的椭圆E经过点G，求点G的纵坐标.
（2）在（1）的条件下，当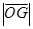取最小值时，求椭圆E的标准方程.
（3）在（2）的条件下，设点A、B分别为椭圆E的左、右顶点，点C是椭圆的下顶点，点P在椭圆E上（与点A、B均不重合），点D在直线PA上，若直线PB的方程为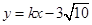，且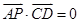，试求CD直线方程.
粤公网安备 44130202000953号