已知 ,函数
,函数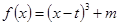 .
.
(1)当 时,若
时,若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若关于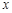 的不等式
的不等式 在区间
在区间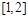 上有解,求
上有解,求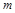 的取值范围;
的取值范围;
(3)已知曲线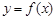 在其图象上的两点
在其图象上的两点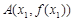 ,
,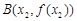 (
(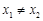 )处的切线分别为
)处的切线分别为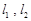 .若直线
.若直线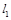 与
与 平行,试探究点
平行,试探究点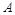 与点
与点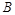 的关系,并证明你的结论.
的关系,并证明你的结论.
推荐套卷
已知 ,函数
,函数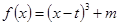 .
.
(1)当 时,若
时,若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若关于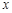 的不等式
的不等式 在区间
在区间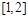 上有解,求
上有解,求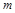 的取值范围;
的取值范围;
(3)已知曲线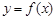 在其图象上的两点
在其图象上的两点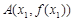 ,
,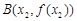 (
(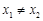 )处的切线分别为
)处的切线分别为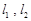 .若直线
.若直线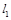 与
与 平行,试探究点
平行,试探究点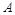 与点
与点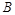 的关系,并证明你的结论.
的关系,并证明你的结论.