抛物线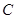 的方程为
的方程为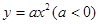 ,过抛物线
,过抛物线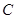 上一点
上一点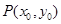 (
( )作斜率为
)作斜率为 的两条直线分别交抛物线
的两条直线分别交抛物线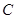 于
于 两点(
两点(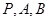 三点互不相同),且满足
三点互不相同),且满足 (
( 且
且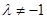 ).
).
(1)求抛物线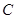 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(2)设直线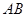 上一点
上一点 ,满足
,满足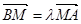 ,证明线段
,证明线段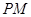 的中点在
的中点在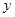 轴上;
轴上;
(3)当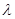 =1时,若点
=1时,若点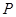 的坐标为
的坐标为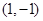 ,求
,求 为钝角时点
为钝角时点 的纵坐标
的纵坐标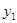 的取值范围.
的取值范围.
相关知识点
推荐套卷
抛物线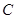 的方程为
的方程为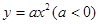 ,过抛物线
,过抛物线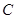 上一点
上一点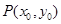 (
( )作斜率为
)作斜率为 的两条直线分别交抛物线
的两条直线分别交抛物线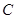 于
于 两点(
两点(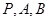 三点互不相同),且满足
三点互不相同),且满足 (
( 且
且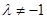 ).
).
(1)求抛物线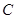 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(2)设直线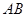 上一点
上一点 ,满足
,满足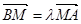 ,证明线段
,证明线段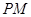 的中点在
的中点在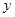 轴上;
轴上;
(3)当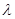 =1时,若点
=1时,若点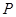 的坐标为
的坐标为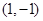 ,求
,求 为钝角时点
为钝角时点 的纵坐标
的纵坐标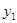 的取值范围.
的取值范围.