如图：已知△ABC中，AB=5，BC=3，AC=4，PQ∥AB，P点在AC上（与A、C不重合），Q在BC上．
（1）当△PQC的面积是四边形PABQ的面积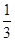
时，求CP的长．
（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长．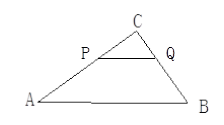
为
上一点，点
分别在
，
，
．求证：
． 
，其中
相关知识点
推荐套卷
如图：已知△ABC中，AB=5，BC=3，AC=4，PQ∥AB，P点在AC上（与A、C不重合），Q在BC上．
（1）当△PQC的面积是四边形PABQ的面积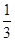时，求CP的长．
（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长．
粤公网安备 44130202000953号