关于函数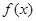 的性质叙述如下:①
的性质叙述如下:①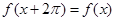 ;②
;②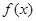 没有最大值;③
没有最大值;③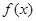 在区间
在区间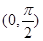 上单调递增;④
上单调递增;④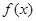 的图象关于原点对称.问:
的图象关于原点对称.问:
(1)函数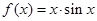 符合上述那几条性质?请对照以上四条性质逐一说明理由.
符合上述那几条性质?请对照以上四条性质逐一说明理由.
(2)是否存在同时符合上述四个性质的函数?若存在,请写出一个这样的函数;若不存在,请说明理由.
推荐套卷
关于函数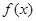 的性质叙述如下:①
的性质叙述如下:①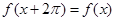 ;②
;②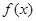 没有最大值;③
没有最大值;③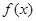 在区间
在区间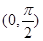 上单调递增;④
上单调递增;④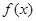 的图象关于原点对称.问:
的图象关于原点对称.问:
(1)函数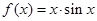 符合上述那几条性质?请对照以上四条性质逐一说明理由.
符合上述那几条性质?请对照以上四条性质逐一说明理由.
(2)是否存在同时符合上述四个性质的函数?若存在,请写出一个这样的函数;若不存在,请说明理由.