一种十字绣作品由相同的小正方形构成，图①，②，③，④分别是制作该作品前四步时对应的图案，按照如此规律，第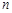
步完成时对应图案中所包含小正方形的个数记为
．
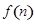① ② ③ ④
（1）求出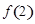
，
，
，
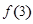的值；
（2）利用归纳推理，归纳出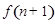
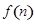与的关系式；
（3）猜想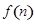的表达式，并写出推导过程．
，且AB、CD在
。
、
，
，
，
为
中点，
，
，
，
，
，
，求：
为
中点。
中，已知
，求异面直线
与
所成角的余弦值 。
相关知识点
推荐套卷
一种十字绣作品由相同的小正方形构成，图①，②，③，④分别是制作该作品前四步时对应的图案，按照如此规律，第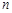步完成时对应图案中所包含小正方形的个数记为．
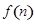① ② ③ ④
（1）求出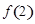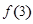，，，的值；
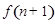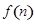（2）利用归纳推理，归纳出与的关系式；
（3）猜想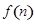的表达式，并写出推导过程．
粤公网安备 44130202000953号