为培养高中生综合实践能力和团队合作意识，某市教育部门主办了全市高中生综合实践知识与技能竞赛.该竞赛分为预赛和决赛两个阶段，参加决赛的团队按照抽签方式决定出场顺序.通过预赛，共选拔出甲、乙等六个优秀团队参加决赛.
（Ⅰ）求决赛出场的顺序中，甲不在第一位、乙不在第六位的概率；
（Ⅱ）若决赛中甲队和乙队之间间隔的团队数记为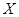
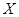，求的分布列和数学期望.
相关试题
的函数
是奇函数。
的值；
的单调性;
，不等式
恒成立，求
的取值范围．
在区间
上有最大值
，求实数
的值
（
）
的定义域。
的关系，并就此说明函数
的点的
的取值范围。
的值域
推荐套卷
为培养高中生综合实践能力和团队合作意识，某市教育部门主办了全市高中生综合实践知识与技能竞赛.该竞赛分为预赛和决赛两个阶段，参加决赛的团队按照抽签方式决定出场顺序.通过预赛，共选拔出甲、乙等六个优秀团队参加决赛.
（Ⅰ）求决赛出场的顺序中，甲不在第一位、乙不在第六位的概率；
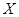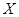（Ⅱ）若决赛中甲队和乙队之间间隔的团队数记为，求的分布列和数学期望.
粤公网安备 44130202000953号