设进入某商场的每一位顾客购买甲种商品的概率为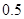 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记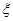 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求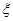 的分布列及期望。
的分布列及期望。
推荐套卷
设进入某商场的每一位顾客购买甲种商品的概率为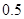 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记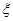 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求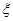 的分布列及期望。
的分布列及期望。