如图，四边形ABCD中，AB⊥AD，AD∥BC，AD＝8，BC＝6，AB＝2，E、F分别在BC、AD上，EF∥AB．现将四边形ABEF沿EF折起，使得平面ABEF
平面EFDC．
（Ⅰ）当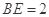
，是否在折叠后的AD上存在一点
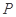，且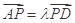
，使得CP∥平面ABEF？若存在，求出
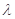的值；若不存在，说明理由；
（Ⅱ）设BE＝x，问当x为何值时，三棱锥A
CDF的体积有最大值？并求出这个最大值．
相关试题
中，内角
对边的边长分别是
，已知
，
．
，求
；
，求
的最小正周期和图象的对称轴方程
上的值域
)2+lg
·lg5+
;
=
,求
的值
，（
，且
）．
的定义域；
的取值范围．
，
，
，其中
． 
时，求
值的集合； 
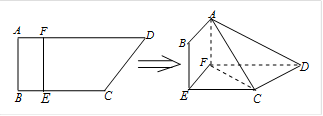
的最大值．推荐套卷
如图，四边形ABCD中，AB⊥AD，AD∥BC，AD＝8，BC＝6，AB＝2，E、F分别在BC、AD上，EF∥AB．现将四边形ABEF沿EF折起，使得平面ABEF平面EFDC．
（Ⅰ）当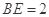，是否在折叠后的AD上存在一点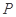，且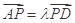，使得CP∥平面ABEF？若存在，求出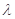的值；若不存在，说明理由；
（Ⅱ）设BE＝x，问当x为何值时，三棱锥ACDF的体积有最大值？并求出这个最大值．
粤公网安备 44130202000953号