某校兴趣小组进行了一项“娱乐与年龄关系”的调查，对 15～65岁的人群随机抽取1000人的样本，进行了一次“是否是电影明星追星族”调查，得到如下各年龄段样本人数频率分布直方图和“追星族”统计表：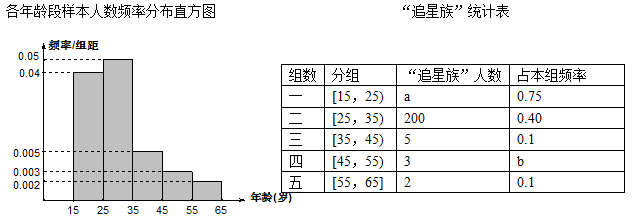
（1）求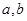
的值．
（2）设从45岁到65岁的人群中，随机抽取2人，用样本数据估计总体，
表示其中“追星族”的人数，求分布列、期望和方差．
,
),且0＜
，求不等式qx2+px+1＞0的解集.
＜0 （a∈R）.推荐套卷
某校兴趣小组进行了一项“娱乐与年龄关系”的调查，对 15～65岁的人群随机抽取1000人的样本，进行了一次“是否是电影明星追星族”调查，得到如下各年龄段样本人数频率分布直方图和“追星族”统计表：
（1）求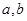的值．
（2）设从45岁到65岁的人群中，随机抽取2人，用样本数据估计总体，表示其中“追星族”的人数，求分布列、期望和方差．
粤公网安备 44130202000953号