三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若 ,
, ,PB与底面ABC成60°角,
,PB与底面ABC成60°角, 分别是
分别是 与
与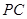 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体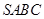 的体积.
的体积.
相关知识点
推荐套卷
三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若 ,
, ,PB与底面ABC成60°角,
,PB与底面ABC成60°角, 分别是
分别是 与
与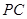 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体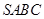 的体积.
的体积.