某渔场鱼群的最大养殖量为 吨,为保证鱼群的生长空间,实际养殖量
吨,为保证鱼群的生长空间,实际养殖量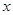 要小于
要小于 ,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量
,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量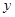 (
(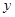 吨)和实际养殖量
吨)和实际养殖量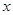 (吨)与空闲率的乘积成正比(设比例系数
(吨)与空闲率的乘积成正比(设比例系数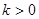 )。
)。
(1)写出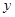 与
与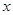 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群年增长量达到最大值时,求 的取值范围.
的取值范围.
推荐套卷
某渔场鱼群的最大养殖量为 吨,为保证鱼群的生长空间,实际养殖量
吨,为保证鱼群的生长空间,实际养殖量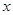 要小于
要小于 ,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量
,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量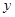 (
(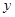 吨)和实际养殖量
吨)和实际养殖量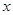 (吨)与空闲率的乘积成正比(设比例系数
(吨)与空闲率的乘积成正比(设比例系数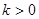 )。
)。
(1)写出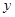 与
与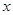 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群年增长量达到最大值时,求 的取值范围.
的取值范围.