如图①,直角三角形AOB中,∠AOB=90°,AB平行于x轴,OA=2OB,AB=5,反比例函数 的图象经过点A.
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过O 作OQ⊥OP,且OP=2OQ,连接PQ.设Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.
相关知识点
推荐套卷
 ,
, (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式; ,试求t的取值范围.
,试求t的取值范围.
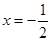 时,y的值.
时,y的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号