（本小题满分12分）
某工厂生产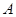
、
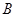两种产品，计划每种产品的生产量不少于15千克，已知生产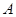产品1千克要用煤9吨，电力4千瓦，3个工作日；生产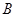产品1千克要用煤4吨，电力5千瓦，10个工作日。又知生产出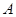产品1千克可获利7万元，生产出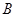产品1千克可获利12万元，现在工厂只有煤360吨，电力200千瓦，300个工作日，
（1）列出满足题意的不等式组，并画图；
（2）在这种情况下,生产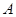、B产品各多少千克能获得最大经济效益.
相关试题
,且
,命题
,且
.
,求实数
的值；
是
的充分条件,求实数
，
.
，求函数
在区间
上的最值；
恒成立，求
的取值范围. （注：
是自然对数的底数）
是定义域为
的奇函数．
的值；
，且
在
上的最小值为
，求
的值.
．
时，求函数
的极值；
上单调递增，试求
的取值或取值范围
方程
在[－1,1]上有解；命题
只有一个实数
满足不等式
，若命题“p∨q”是假命题，求实数
的取值范围．推荐套卷
（本小题满分12分）
某工厂生产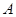、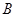两种产品，计划每种产品的生产量不少于15千克，已知生产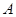产品1千克要用煤9吨，电力4千瓦，3个工作日；生产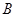产品1千克要用煤4吨，电力5千瓦，10个工作日。又知生产出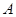产品1千克可获利7万元，生产出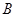产品1千克可获利12万元，现在工厂只有煤360吨，电力200千瓦，300个工作日，
（1）列出满足题意的不等式组，并画图；
（2）在这种情况下,生产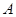、B产品各多少千克能获得最大经济效益.
粤公网安备 44130202000953号