为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了10名同学参加决赛(满分为100分)如表所示:
决赛成绩(单位:分)
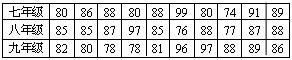
(1)请你填写下表:

(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
从平均数和众数相结合看(分析哪个年级成绩好些):_________;
从平均数和中位数相结合看(分析哪个年级成绩好些):___________;
(3)如果在每个年级参加决赛的选手中分别选出三人参加决赛,你认为哪个年级的实力更强一些。说明理由:__________________________________________________________。