如图,在矩形 ABCD中, AB=3, BC=5, E是 AD上的一个动点. 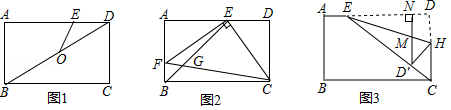
(1)如图1,连接 BD, O是对角线 BD的中点,连接 OE.当 OE= DE时,求 AE的长;
(2)如图2,连接 BE, EC,过点 E作 EF⊥ EC交 AB于点 F,连接 CF,与 BE交于点 G.当 BE平分∠ ABC时,求 BG的长;
(3)如图3,连接 EC,点 H在 CD上,将矩形 ABCD沿直线 EH折叠,折叠后点 D落在 EC上的点 D'处,过点 D′作 D′ N⊥ AD于点 N,与 EH交于点 M,且 AE=1.
①求
的值;
②连接 BE,△ D' MH与△ CBE是否相似?请说明理由.