如图,在平面直角坐标系xOy中,直线 与
与 轴交于点A(
轴交于点A( ,0),与
,0),与 轴交于点B,且与直线
轴交于点B,且与直线 :
: 的交点为C(
的交点为C(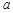 ,4) .
,4) .
(1)求直线 的解析式;
的解析式;
(2)如果以点O,D,B,C为顶点的四边形是平行四边 形,直接写出点D的坐标;
(3)将直线 沿y轴向下平移3个单位长度得到直线
沿y轴向下平移3个单位长度得到直线 ,点P(m,n)为直线
,点P(m,n)为直线 上一动点,过点P作x轴的垂线, 分别与直线
上一动点,过点P作x轴的垂线, 分别与直线 ,
, 交于M,N.当点P在线段MN上时,请直接写出m的取值范围.
交于M,N.当点P在线段MN上时,请直接写出m的取值范围. 
相关知识点
推荐套卷
如图,在平面直角坐标系xOy中,直线 与
与 轴交于点A(
轴交于点A( ,0),与
,0),与 轴交于点B,且与直线
轴交于点B,且与直线 :
: 的交点为C(
的交点为C(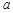 ,4) .
,4) .
(1)求直线 的解析式;
的解析式;
(2)如果以点O,D,B,C为顶点的四边形是平行四边 形,直接写出点D的坐标;
(3)将直线 沿y轴向下平移3个单位长度得到直线
沿y轴向下平移3个单位长度得到直线 ,点P(m,n)为直线
,点P(m,n)为直线 上一动点,过点P作x轴的垂线, 分别与直线
上一动点,过点P作x轴的垂线, 分别与直线 ,
, 交于M,N.当点P在线段MN上时,请直接写出m的取值范围.
交于M,N.当点P在线段MN上时,请直接写出m的取值范围. 