扇形AOB中心角为60°，所在圆半径为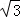
，它按如下（Ⅰ）（Ⅱ）两种方式有内接矩形CDEF．
（Ⅰ）矩形CDEF的顶点C、D在扇形的半径OB上，顶点E在圆弧AB上，顶点F在半径OA上，设∠EOB=θ；
（Ⅱ）点M是圆弧AB的中点，矩形CDEF的顶点D、E在圆弧AB上，且关于直线OM对称，顶点C、F分别在半径OB、OA上，设∠EOM=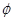
；
试研究（Ⅰ）（Ⅱ）两种方式下矩形面积的最大值，并说明两种方式下哪一种矩形面积最大？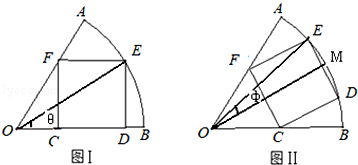
相关试题
中，设
，
，又
，
，向量
，
的夹角为
．
表示
；
．
，
分别是与x轴，y轴方向相同的两个单位向量，
, 
,
,
；
，
的坐标．
中，角
为锐角,记角
所对的边分别为
，设向量
，且
与
的夹角为
．
的值并求角
，求
．
}的公差
，
，且
，
，
成等比数列．
及通项
的前
项和
中，角
所对的边分别为
，已知
,
，
．
的值；
的值．推荐套卷
扇形AOB中心角为60°，所在圆半径为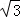，它按如下（Ⅰ）（Ⅱ）两种方式有内接矩形CDEF．
（Ⅰ）矩形CDEF的顶点C、D在扇形的半径OB上，顶点E在圆弧AB上，顶点F在半径OA上，设∠EOB=θ；
（Ⅱ）点M是圆弧AB的中点，矩形CDEF的顶点D、E在圆弧AB上，且关于直线OM对称，顶点C、F分别在半径OB、OA上，设∠EOM=；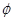
试研究（Ⅰ）（Ⅱ）两种方式下矩形面积的最大值，并说明两种方式下哪一种矩形面积最大？
粤公网安备 44130202000953号