厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验,求至少有1件是合格品的概率;
(2)若厂家发给商家20件产品,其中有3件不合格.按合同规定该商家从中任取2件进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数ξ的分布列及数学期望E(ξ),并求该商家拒收这批产品的概率.
相关知识点
推荐套卷
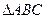 中,角
中,角 所对的边分别为
所对的边分别为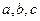 ,且满足
,且满足 ,
,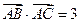 .
. ,求
,求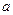 的值.
的值.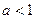 ,解关于
,解关于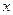 的不等式
的不等式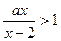 .
.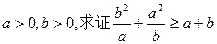

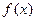 =cos(x+
=cos(x+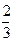 π)+cos
π)+cos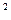
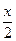 ,0<x<π
,0<x<π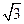 ,求边a的值
,求边a的值 粤公网安备 44130202000953号
粤公网安备 44130202000953号