某电脑经销商计划购进一批电脑机箱和液晶显示器,已知购进电脑机箱10台和液晶显示器8台,共需要资金7000元;购进电脑机箱2台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?
相关知识点
推荐套卷
 为
为 上一点,点
上一点,点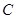 在直径
在直径 的延长线上,
的延长线上,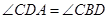 .
.
 是
是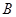 作
作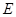 ,若BC=4,tan∠ABD=
,若BC=4,tan∠ABD=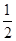 求
求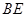 的长.
的长.

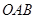 的顶点
的顶点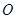 、
、 、
、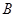 均在格点上,且
均在格点上,且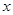 轴上.
轴上.
 与△
与△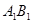 所在直线的函数关系式.
所在直线的函数关系式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号