阅读学习: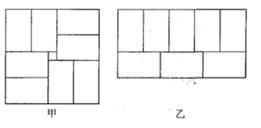
数学中有很多等式可以用图形的面积来表示.如图1,它表示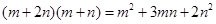 ,
,
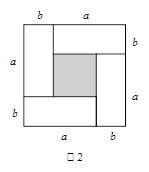
(1)观察图2,请你写出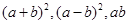 之间的关系________________________.
之间的关系________________________.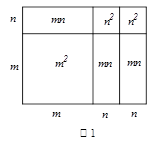
(2)小明用8个一样大的长方形,(长为a,宽为b),拼成了如图甲乙两种图案,图案甲是一个正方形,图案甲中间留下了一个边长为2的正方形;图形乙是一个长方形.则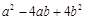 ="___________"
="___________"
阅读学习:
数学中有很多等式可以用图形的面积来表示.如图1,它表示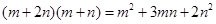 ,
,
(1)观察图2,请你写出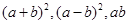 之间的关系________________________.
之间的关系________________________.

(2)小明用8个一样大的长方形,(长为a,宽为b),拼成了如图甲乙两种图案,图案甲是一个正方形,图案甲中间留下了一个边长为2的正方形;图形乙是一个长方形.则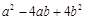 ="___________"
="___________"