在直角坐标系xOy中，直线l的方程为x-y+4=0，
曲线C的参数方程为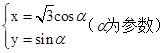 
．
（Ⅰ）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，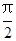
），判断点P与直线l的位置关系；
（Ⅱ）设点Q是曲线C上的一个动点，求它到直线l的距离的最值．
（Ⅲ）请问是否存在直线m ， m∥l且m与曲线C的交点A、B满足
；
若存在请求出满足题意的所有直线方程，若不存在请说明理由。
－1)x＋m＝0的两根．
＋
的值．
·
.
，其中α为第三象限角，求cos(105°－α)＋sin(α－105°)的值．
.
，求下列各式的值．
；相关知识点
推荐套卷
在直角坐标系xOy中，直线l的方程为x-y+4=0，
曲线C的参数方程为 ．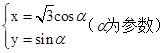
（Ⅰ）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4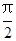，），判断点P与直线l的位置关系；
（Ⅱ）设点Q是曲线C上的一个动点，求它到直线l的距离的最值．
（Ⅲ）请问是否存在直线m ， m∥l且m与曲线C的交点A、B满足；
若存在请求出满足题意的所有直线方程，若不存在请说明理由。
粤公网安备 44130202000953号