(本小题满分12分)
某客运公司争取到一个相距100海里的甲、乙两地的客运航线权。已知轮船的平均载客人数为200人,轮船每小时使用的燃料费和轮船航行速度的平方成正比,轮船的最大速度为20海里/小时,当船速为10海里/小时,它的燃料费用是每小时60元,其余费用(不论速度如何)总计是每小时150元,假定轮船从甲地到乙地匀速航行。
(I)求轮船每小时的燃料费W与速度v的关系式;
(II)若公司打算从每位乘客身上获得利润10元,那么该公司设计的船票价格最低可以是多少?(精确到1元,参考数据: )
)
相关知识点
推荐套卷
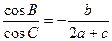 ,
,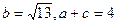 ,求△ABC的面积。
,求△ABC的面积。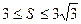 且
且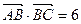 ,
,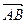 与
与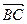 的夹角为
的夹角为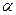
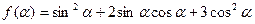 的最小值。
的最小值。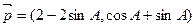 与向量
与向量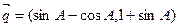 是共线向量,
是共线向量,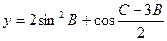 的最大值。
的最大值。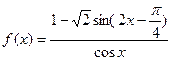 ,(1)求
,(1)求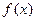 的定义域;
的定义域;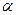 是第四象限的角,且
是第四象限的角,且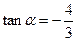 ,求
,求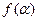 的值。
的值。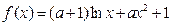 .
.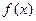 的单调性;
的单调性;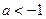 ,如果对任意
,如果对任意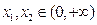 ,
,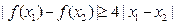 ,求
,求 的取值范围
的取值范围 粤公网安备 44130202000953号
粤公网安备 44130202000953号