某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含
个小正方形.
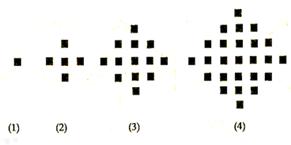
（Ⅰ）求出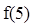
；
（Ⅱ）利用合情推理的“归纳推理思想”归纳出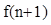
与
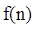的关系式，
（Ⅲ）根据你得到的关系式求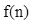
的表达式.
，化简
＋
.
＝
且
<x<
，求
的值．
.
为实数，函数
。
，求
的最小值
，直接写出（不需要给出演算步骤）不等式
的解集。
，若函数
的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数
的图象：
的解析式
，讨论
的单调性
时，总有
成立，求实数
的取值范围。相关知识点
推荐套卷
某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含个小正方形.
（Ⅰ）求出；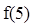
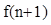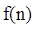（Ⅱ）利用合情推理的“归纳推理思想”归纳出与的关系式，
（Ⅲ）根据你得到的关系式求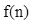的表达式.
粤公网安备 44130202000953号