如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到△ABC,然后将此三角形向下平移4个单位,再画出平移后的△A′B′C′,并计算△A′B′C′的面积﹒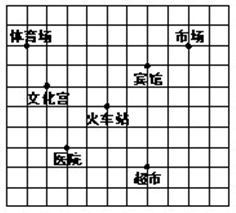
相关知识点
推荐套卷
如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到△ABC,然后将此三角形向下平移4个单位,再画出平移后的△A′B′C′,并计算△A′B′C′的面积﹒