某校夏令营有3名男同学
和3名女同学
，其年级情况如下表：
| |
一年级 |
二年级 |
三年级 |
| 男同学 |
 |
 |
 |
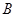| 女同学 |
 |
 |
 |
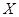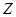现从这6名同学中随机选出2人参加知识竞赛（每人被选到的可能性相同）
（1）用表中字母列举出所有可能的结果
（2）设
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件发生的概率.
的定义域为
，且对任意
，都有
，且当
时，
恒成立，
（2）
的前
项和
，求数列
是奇函数的充要条件是
。
是
的充分条件，而
的必要条件，
的充分条件，推荐套卷
某校夏令营有3名男同学和3名女同学，其年级情况如下表：
| |
一年级 |
二年级 |
三年级 |
| 男同学 |
|
|
|
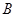| 女同学 |
|
|
|
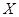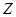现从这6名同学中随机选出2人参加知识竞赛（每人被选到的可能性相同）
（1）用表中字母列举出所有可能的结果
（2）设为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件发生的概率.
粤公网安备 44130202000953号