某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求该同学看中的随身听和书包单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),该同学只带了400元钱,他能否在这两家超市都可以买下看中的这两样商品?若两家都可以选择,在哪一家购买更省钱?
相关知识点
推荐套卷
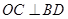 于点M,CF⊥AB于点F交BD于点E,
于点M,CF⊥AB于点F交BD于点E,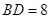 ,
,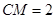
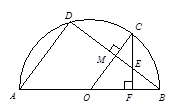
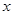 的方程
的方程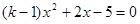 有两个不相等的实数根,
有两个不相等的实数根, 的取值范围.②当k为最小整数时求原方程的解。
的取值范围.②当k为最小整数时求原方程的解。
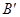 的坐标;
的坐标;

 粤公网安备 44130202000953号
粤公网安备 44130202000953号