如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y= (x>0)的函数图象经过点D,点P是一次函数
(x>0)的函数图象经过点D,点P是一次函数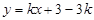
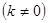 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数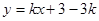
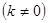 的图象一定过点C;
的图象一定过点C;
(3)对于一次函数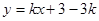
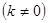 ,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).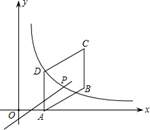
推荐套卷
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y= (x>0)的函数图象经过点D,点P是一次函数
(x>0)的函数图象经过点D,点P是一次函数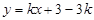
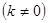 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数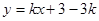
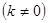 的图象一定过点C;
的图象一定过点C;
(3)对于一次函数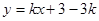
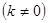 ,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).