某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：
，绘制成如图所示的频率分布直方图.
（1）求直方图中
的值；
（2）求续驶里程在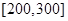
的车辆数；
（3）若从续驶里程在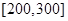的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为
的概率.
相关试题
，求b的值
满足
，
，
。
是等差数列
的极值点，求实数a的值；
上为增函数，求实数a的取值范围；
有实根，求实数b的最大值。推荐套卷
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：，绘制成如图所示的频率分布直方图.
（1）求直方图中的值；
（2）求续驶里程在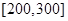的车辆数；
（3）若从续驶里程在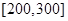的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为的概率.
粤公网安备 44130202000953号