某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与 元成反比例.又当
元成反比例.又当 时,
时,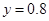 .
.
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益 用电量
用电量 (实际电价-成本价)]
(实际电价-成本价)]
推荐套卷
某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与 元成反比例.又当
元成反比例.又当 时,
时,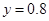 .
.
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益 用电量
用电量 (实际电价-成本价)]
(实际电价-成本价)]