如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.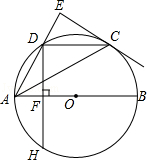
推荐套卷
如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.