如图，已知直线l1∥l2，线段AB在直线l1上，BC垂直于l1交l2于点C，且AB=BC，P是线段BC上异于两端点的一点，过点P的直线分别交l2、l1于点D、E（点A、E位于点B的两侧），满足BP=BE，连接AP、CE．
（1）求证：△ABP≌△CBE；
（2）连结AD、BD，BD与AP相交于点F．如图2．
①当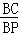
=2时，求证：AP⊥BD；
②当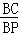=n（n＞1）时，设△PAD的面积为S1，△PCE的面积为S2，求
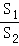的值．
＋
的值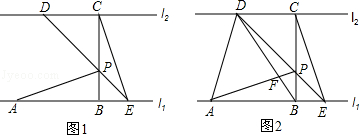．相关知识点
推荐套卷
如图，已知直线l1∥l2，线段AB在直线l1上，BC垂直于l1交l2于点C，且AB=BC，P是线段BC上异于两端点的一点，过点P的直线分别交l2、l1于点D、E（点A、E位于点B的两侧），满足BP=BE，连接AP、CE．
（1）求证：△ABP≌△CBE；
（2）连结AD、BD，BD与AP相交于点F．如图2．
①当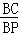=2时，求证：AP⊥BD；
②当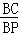=n（n＞1）时，设△PAD的面积为S1，△PCE的面积为S2，求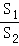的值．
粤公网安备 44130202000953号