如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再次测得A在C的北偏西45°的方向上（其中A、B、C在同一平面上）．求这个标志性建筑物底部A到岸边BC的最短距离．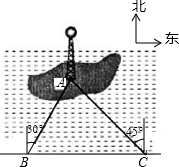
，求分式
的值：
，试求
的值
相关知识点
推荐套卷
如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再次测得A在C的北偏西45°的方向上（其中A、B、C在同一平面上）．求这个标志性建筑物底部A到岸边BC的最短距离．
粤公网安备 44130202000953号