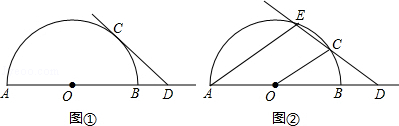已知AB是半圆O的直径，点C是半圆O上的动点，点D是线段AB延长线上的动点，在运动过程中，保持CD=OA．
（1）当直线CD与半圆O相切时（如图①），求∠ODC的度数；
（2）当直线CD与半圆O相交时（如图②），设另一交点为E，连接AE，若AE∥OC，
①AE与OD的大小有什么关系？为什么？
②求∠ODC的度数．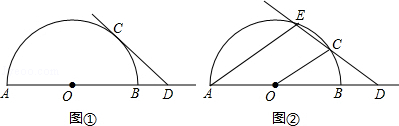
相关试题
外一点，且BD=CD，
，点M，N分别在AB,AC上，若
,
的高DH，并证明DH=BD;
中，AD平分
且平分BC交BC于G，
于E,
交AC的延长线于F.
，求AE、BE的长.
中，AB=BC，
，D是AB上一点，AE⊥CD交其延长线于点E，且
,求D到AC的距离。
是
的算术平方根，
为
的立方根，求
的立方根；
相关知识点
推荐套卷
已知AB是半圆O的直径，点C是半圆O上的动点，点D是线段AB延长线上的动点，在运动过程中，保持CD=OA．
（1）当直线CD与半圆O相切时（如图①），求∠ODC的度数；
（2）当直线CD与半圆O相交时（如图②），设另一交点为E，连接AE，若AE∥OC，
①AE与OD的大小有什么关系？为什么？
②求∠ODC的度数．
粤公网安备 44130202000953号