如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH="2cm," GK="2cm," 设BF="x" cm,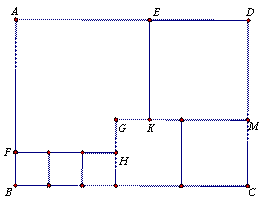
(1)用含x的代数式表示CM=_____________cm,DM=_____________cm.
(2)若DC=10cm,求x的值.
(3)求长方形ABCD的面积.
相关知识点
推荐套卷
如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH="2cm," GK="2cm," 设BF="x" cm,
(1)用含x的代数式表示CM=_____________cm,DM=_____________cm.
(2)若DC=10cm,求x的值.
(3)求长方形ABCD的面积.