实验北校举行运动会,组委会招墓了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10 人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下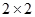 列联表:
列联表:
(2)根据列联表的独立性检验,有多大的把握认为性别与喜爱运动有关?
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人,求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率.
参考公式 :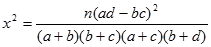 (其中
(其中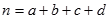 )
)
| |
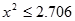 |
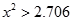 |
 |
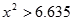 |
| 是否有关联 |
没有关联 |
90% |
95% |
99% |
推荐套卷
 度的人数如下表:
度的人数如下表: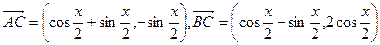 ,设
,设 =
= (1).求
(1).求 的方程
的方程 在
在 有两个不相等的实数根,求
有两个不相等的实数根,求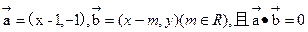

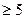
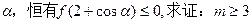
 x,y)表示点P的坐标,其中x表示第1颗骰子出现的点数,y表示第2颗骰子出现的点数.
x,y)表示点P的坐标,其中x表示第1颗骰子出现的点数,y表示第2颗骰子出现的点数.
 点P的坐标(x,y)满足16<
点P的坐标(x,y)满足16< 的概率
的概率 粤公网安备 44130202000953号
粤公网安备 44130202000953号