通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化。类似的，可以在等腰三角形中建立边角之间的联系。我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图①在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA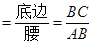
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解下列问题：如图②，已知sinA
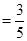，其中∠A为锐角，试求sadA的值。
相关试题
）-1+（
）2013×（-
）2014我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小．而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一，所谓“作差法”：就是通过作差、变形，并利用差的符号来确定它们的大小，即要比较代数式M、N的大小，只要作出它们的差M－N，若M－N＞0，则M＞N；若M－N=0，则M=N．若M－N＜0，则M＜N，
请你用“作差法”解决以下问题：
（1）如图，试比较图①、图②两个矩形的周长C1、C2的大小（b＞c）．
（2）如图③，把边长为a＋b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形的面积之和S1与两个矩形面积之和S2的大小．
（2）解不等式组
相关知识点
推荐套卷
粤公网安备 44130202000953号