将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.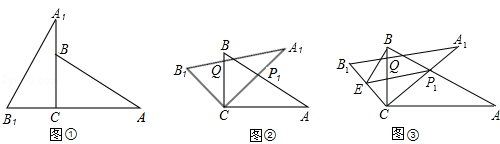
推荐套卷
将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.