设项数均为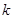 (
(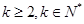 )的数列
)的数列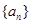 、
、 、
、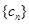 前
前 项的和分别为
项的和分别为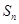 、
、 、
、 .已知
.已知 ,且集合
,且集合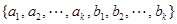 =
=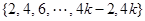 .
.
(1)已知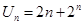 ,求数列
,求数列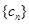 的通项公式;
的通项公式;
(2)若 ,求
,求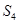 和
和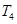 的值,并写出两对符合题意的数列
的值,并写出两对符合题意的数列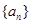 、
、 ;
;
(3)对于固定的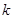 ,求证:符合条件的数列对(
,求证:符合条件的数列对(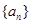 ,
, )有偶数对.
)有偶数对.
推荐套卷
设项数均为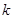 (
(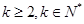 )的数列
)的数列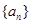 、
、 、
、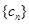 前
前 项的和分别为
项的和分别为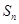 、
、 、
、 .已知
.已知 ,且集合
,且集合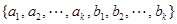 =
=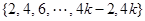 .
.
(1)已知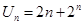 ,求数列
,求数列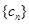 的通项公式;
的通项公式;
(2)若 ,求
,求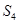 和
和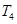 的值,并写出两对符合题意的数列
的值,并写出两对符合题意的数列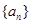 、
、 ;
;
(3)对于固定的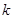 ,求证:符合条件的数列对(
,求证:符合条件的数列对(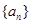 ,
, )有偶数对.
)有偶数对.