某电视台“挑战60秒”活动规定上台演唱: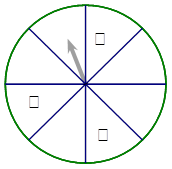
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).
(II)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(III)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
(1)求此人中一等奖的概率;
(2)设此人所得奖金为
,求的分布列及数学期望
.
相关试题
某次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并宣
布：观众答对问题A可获奖金2a元；答对问题B可获奖金3a元，答对两题则可获5a元.先答哪个问题由观众选择，只有第1题答对才能答第2题，否则中止答题.若你被选为幸运观众，且假设你答对A、B的概率分别为
、
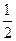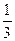，你觉得应先回答哪个问题？说明理由.
A、B两个代表队进行乒乓球对抗赛，每队三名队员，A队队员是A1、A2、A3，B队队员是B1、B2、B3。按以往多次比赛的统计，对阵队员之间胜负概率如下：
| 对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
| A1对B1 |
2 3 |
1 3 |
| A2对B2 |
2 5 |
3 5 |
| A3对B3 |
2 5 |
3 5 |
现按表中对阵方式出场, 每场胜队得1分, 负队得0分,设A队、B队最后总分分别为x、h.
(Ⅰ) 求x、h的概率分布；
(Ⅱ) 求Ex、Eh.
A、B两台机床同时加工零件，每生产一批数量较大的产品时，出次品的概率如下表所示：
A机床 B机床
| 次品数ξ1 |
0 |
1 |
2 |
3 |
| 概率P |
0.7 |
0.2 |
0.06 |
0.04 |
| 次品数ξ2 |
0 |
1 |
2 |
3 |
| 概率P |
0.8 |
0.06 |
0.04 |
0.10 |
问哪一台机床加工质量较好
相关知识点
推荐套卷
粤公网安备 44130202000953号