在平面直角坐标系xoy中，已知椭圆C：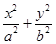
=1（a>b≥1）的离心率e=
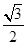，且椭圆C上的点到点Q （0,3）的距离最大值为4，过点M（3，0）的直线交椭圆C于点A、B．
（1）求椭圆C的方程。
（2）设P为椭圆上一点，且满足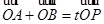
（O为坐标原点），当|AB|<
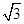时，求实数t的取值范围．
相关试题
中，点E，D分别是
与BC的中点．
EB//平面AD
．
的椭圆
过点
，
是坐
的方程；
为椭圆
，判定直线
与圆
的
在
处取得极值
.
的值；
的方程
在区间
上有实根，求实数
的取值范围.
中，底面
是平行四边形，
侧面
，点
在侧棱
上，且
.
平面
；
所成角为
，二面角
的大小为
，求
与平面
所成角的大小.
推荐套卷
在平面直角坐标系xoy中，已知椭圆C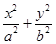：=1（a>b≥1）的离心率e=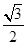，且椭圆C上的点到点Q （0,3）的距离最大值为4，过点M（3，0）的直线交椭圆C于点A、B．
（1）求椭圆C的方程。
（2）设P为椭圆上一点，且满足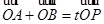（O为坐标原点），当|AB|<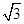时，求实数t的取值范围．
粤公网安备 44130202000953号