设向量
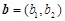 ,定义一种向量积
,定义一种向量积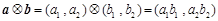 .
.
已知向量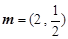 ,
,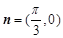 ,点
,点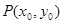 为
为 的图象上的动点,点
的图象上的动点,点 为
为 的图象上的动点,且满足
的图象上的动点,且满足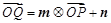 (其中
(其中 为坐标原点).
为坐标原点).
(1)请用 表示
表示 ;
;
(2)求 的表达式并求它的周期;
的表达式并求它的周期;
(3)把函数 图象上各点的横坐标缩小为原来的
图象上各点的横坐标缩小为原来的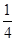 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象.设函数
的图象.设函数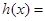
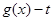
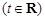 ,试讨论函数
,试讨论函数 在区间
在区间 内的零点个数.
内的零点个数.
相关知识点
推荐套卷
设向量
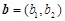 ,定义一种向量积
,定义一种向量积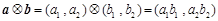 .
.
已知向量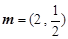 ,
,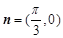 ,点
,点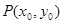 为
为 的图象上的动点,点
的图象上的动点,点 为
为 的图象上的动点,且满足
的图象上的动点,且满足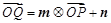 (其中
(其中 为坐标原点).
为坐标原点).
(1)请用 表示
表示 ;
;
(2)求 的表达式并求它的周期;
的表达式并求它的周期;
(3)把函数 图象上各点的横坐标缩小为原来的
图象上各点的横坐标缩小为原来的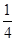 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象.设函数
的图象.设函数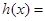
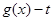
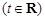 ,试讨论函数
,试讨论函数 在区间
在区间 内的零点个数.
内的零点个数.