已知:甲、乙两车分别从相距300千米的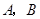 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到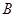 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离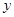 (千米)与行驶时间
(千米)与行驶时间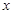 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)求甲车离出发地的距离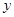 (千米)与行驶时间
(千米)与行驶时间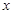 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了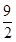 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离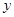 (千米)与行驶时间
(千米)与行驶时间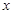 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.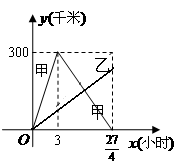
相关知识点
推荐套卷

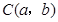 为线段
为线段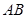 上任一点,写出变化后点
上任一点,写出变化后点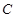 的对应点
的对应点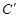 的坐标 ().
的坐标 ().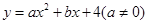 与
与 轴交于点
轴交于点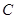 ,与
,与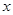 轴交于点
轴交于点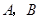 ,点
,点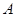 的坐标为
的坐标为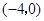 ,对称轴是
,对称轴是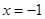 .
.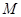 是线段
是线段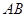 上的动点,过点
上的动点,过点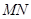 ∥
∥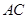 ,分别交
,分别交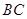 于点P、
于点P、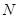 ,连接
,连接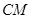 .当
.当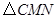 的面积最大时,求点
的面积最大时,求点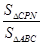 的值.
的值.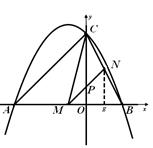
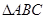 内接于⊙O,
内接于⊙O, 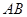 为⊙O的直径,
为⊙O的直径,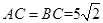 , 点
, 点 是
是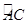 上一个动点,连结
上一个动点,连结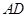 、
、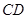 和
和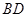 ,
, 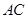 相交于点
相交于点 , 过点
, 过点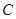 作
作 于
于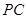 与
与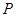 ,连结
,连结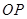 和
和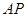 .
.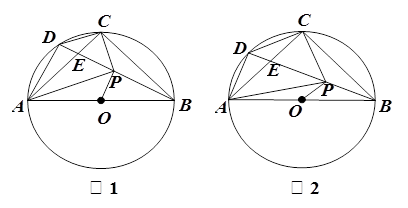
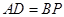 ;
;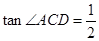 , 求证:
, 求证: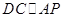 ;
;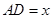 , 四边形
, 四边形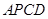 的面积为
的面积为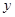 ,求
,求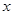 之间的关系式.
之间的关系式.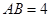 ,
,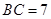 ,点P是AD边上一个动点,
,点P是AD边上一个动点,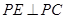 ,
, 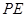 交
交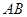 于点
于点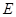 ,对应点
,对应点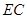 .
.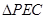 是等腰三角形,求
是等腰三角形,求 的长;
的长; 时,求
时,求 的长.
的长.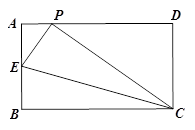
 粤公网安备 44130202000953号
粤公网安备 44130202000953号